第2話 補遺
① 引き算の規則
引き算を含む結合則
足し算の結合則は、
$$ (a+b) +c = a + (b+c)\ , $$
だった。そこで、\(b \rightarrow b-c\) とすると、
$$ \left( a + (b-c)\right) + c = a + \left((b-c)+c\right) \ .$$
引き算の定義 \((b-c)+c = b\) を使うと、右辺は \(a+b\) になる。
$$ \left(a + (b-c)\right) + c = a + b \ .$$
そこで、両辺から \(c\) を引くと、引き算を含む結合則、
$$a+(b-c)=(a+b)-c\ ,$$
が導かれる。
引き算と掛け算の分配則
引き算を足し算の逆と考えると、引き算と掛け算の間にも分配則
$$a\times (b-c)=a\times b-a\times c\ , $$
が成り立つことを示すことができる。
まず、足し算については分配則が成り立つので、
$$a\times \left( (b-c)+c\right)=a\times (b-c)+a\times c \ .$$
となる。
ところが、引き算の定義によって \((b-c)+c=b\) なので、左辺は \(a\times b\) に等しい。つまり、
$$a\times b=a\times (b-c)+a\times c \ .$$
この両辺から \(a\times c\) を引いて、右辺と左辺を入れ替えると、
$$a\times (b-c)=a\times b-a\times c\ .$$
これで、引き算と掛け算についての分配則が導かれた。
② 分数の規則
分数の掛け算
分数の掛け算では、分子同士、分母同士を掛ければよいことを示す。
まず、分数の定義に戻ると、
$$\frac{a}{b} \times b = a\ , ~~\frac{c}{d} \times d =c\ . $$
この2つの式の左辺同士を掛けて、結合則と交換則を使うと、
$$\left(\frac{a}{b} \times b\right) \times \left(\frac{c}{d} \times d\right)=\left( \frac{a}{b} \times \frac{c}{d} \right) \times (b \times d)\ . $$
となる。これが、右辺同士を掛けた \(a \times c\) に等しい。
$$ \left( \frac{a}{b} \times \frac{c}{d} \right) \times (b \times d) = a \times c\ .$$
そこで、両辺を \(b\times d\) で割ると、
$$ \frac{a}{b} \times \frac{c}{d} = \frac{a\times c}{b\times d}\ , $$
となって、「掛け算では、分子同士、分母同士を掛ける」ことが示された。
約分はなぜできる
約分とは、
$$ \frac{a\times c}{b\times c} = \frac{a}{b}\ ,$$
ということだ。ここで、左辺は \((a\times c)\div (b\times c)\) だから、これは
\(x \times (b\times c) = a \times c\)の解ということだ。
一方、右辺は \(x\times b =a\) の解だ。つまり、約分ができるというのは
$$x \times (b\times c) = a \times c\ ,$$
と
$$x \times b = a\ , $$
という2つの問題の答えが同じだということだ。
実際、\(x\) が \(x\times b =a\) の解だとすると、両辺に \(c\) を掛けて、掛け算の結合則を使うと、\(x \times (b\times c) = a \times c\)になる。つまり、2つの問題の解は同じだ。これで、約分ができることが証明できた。
③ 連分数で最大公約数を見つける
分数を約分するためには、分子と分母の共通の約数、つまり公約数を見つけなければいけない。一番大きな公約数、すなわち「最大公約数」を見つける方法としては、高校の数学で勉強する「ユークリッドの互除法」があるが、ここでは連分数を使った方法を説明しよう。
たとえば、1107と287の最大公約数を求めるために、分数\(1107/287\)を連分数表示してみる。
\begin{align}\frac{1107}{287} & = 3 + \frac{246}{287} \nonumber \\ &= 3+ \cfrac{1}{~~\cfrac{287}{246}~~} \nonumber \\ & = 3 + \cfrac{1}{1 + \cfrac{41}{246}} \nonumber \\ & = 3 + \cfrac{1}{1 + \cfrac{1}{\cfrac{246}{41}}} \ .\nonumber \end{align}
この最後のステップで、分母 \(246/41\) の帯分数表示をしようとすると、\(246/41=6\) と割り切れるので、ここで連分数は終了する。
今の計算では、最後のステップになるまでわざと約分をしなかった。そうすると、一番最後に分子の \(246\) が分母の \(41\) で割り切れて \(6\) となる。これをさかのぼっていくと、そもそも、最初の \(1107/287\) の分子と分母の最大公約数が \(41\) で、それで約分すると \(1107/287=27/7\) だったことがわかる。実際、上の連分数表示で \(246/41=6\) とすると、\(27/7\) の連分数表示、
$$\frac{27}{7} = 3 + \frac{6}{7}= 3 + \cfrac{1}{~~\cfrac{7}{6}~~ }= 3 + \cfrac{1}{1 + \cfrac{1}{6}} \ , $$
と同じになる。
どんな分数についても、この連分数を計算する操作をしていくと、現れる分数の分子と分母が小さくなっていく。だから、この操作は必ず終わる。そして、一番最後の操作で明らかになるのが、最初の分子と分母の最大公約数
だ。
実は、この方法は、「ユークリッドの互除法」と同じことだ。ここでは説明しないけれど、たとえば高校の数学の教科書の説明と比較してみると、各々のステップが対応していることがわかるから、興味があったら確認してみよう。
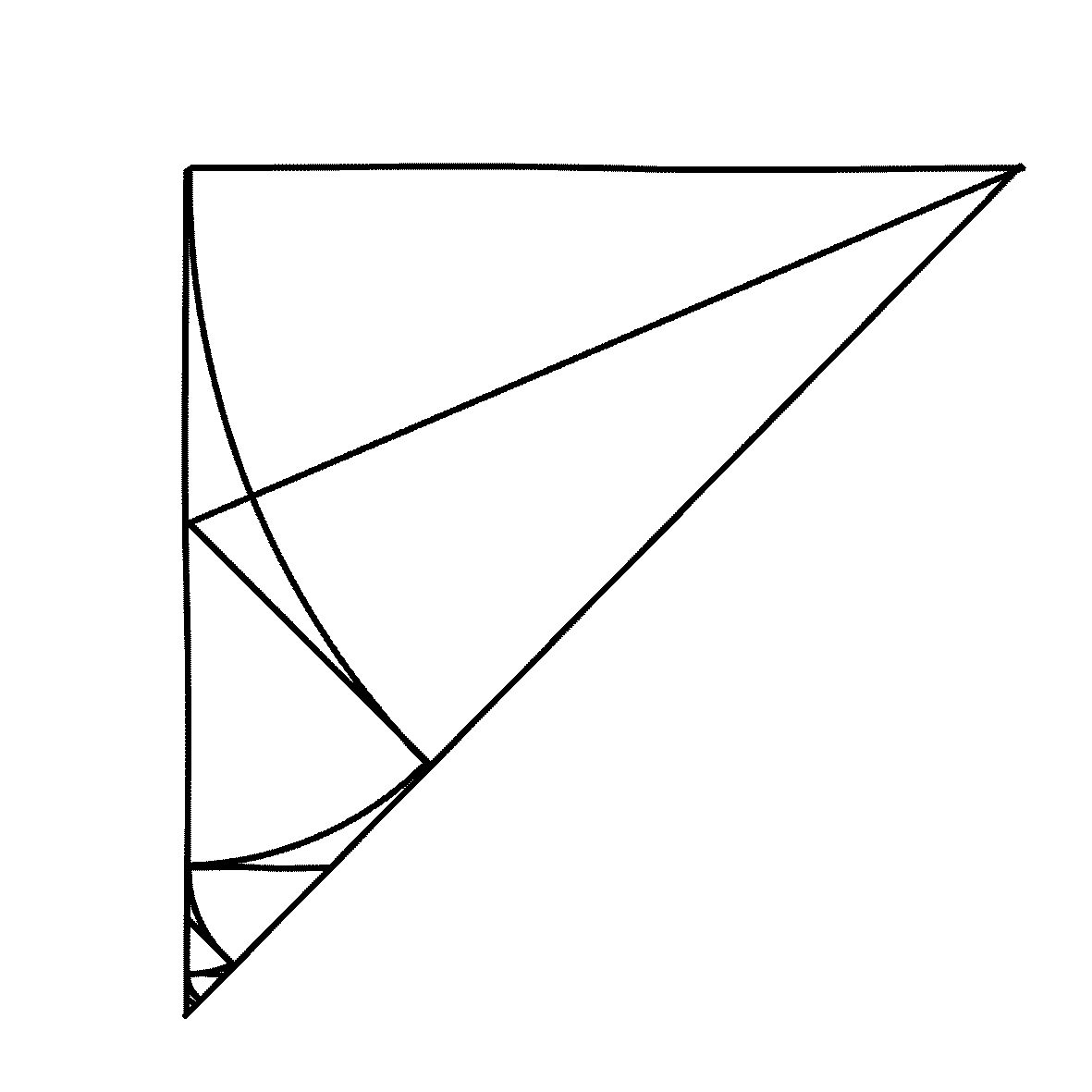
④ \(\sqrt{2}\)が無理数であることの幾何学的証明

上図のような直角2等辺3角形 \(ABC\) を考えると、
$$ \sqrt{2} = \frac{AC}{AB},$$
だ。これが自然数の比として表現できるかを、幾何学的に考えよう。
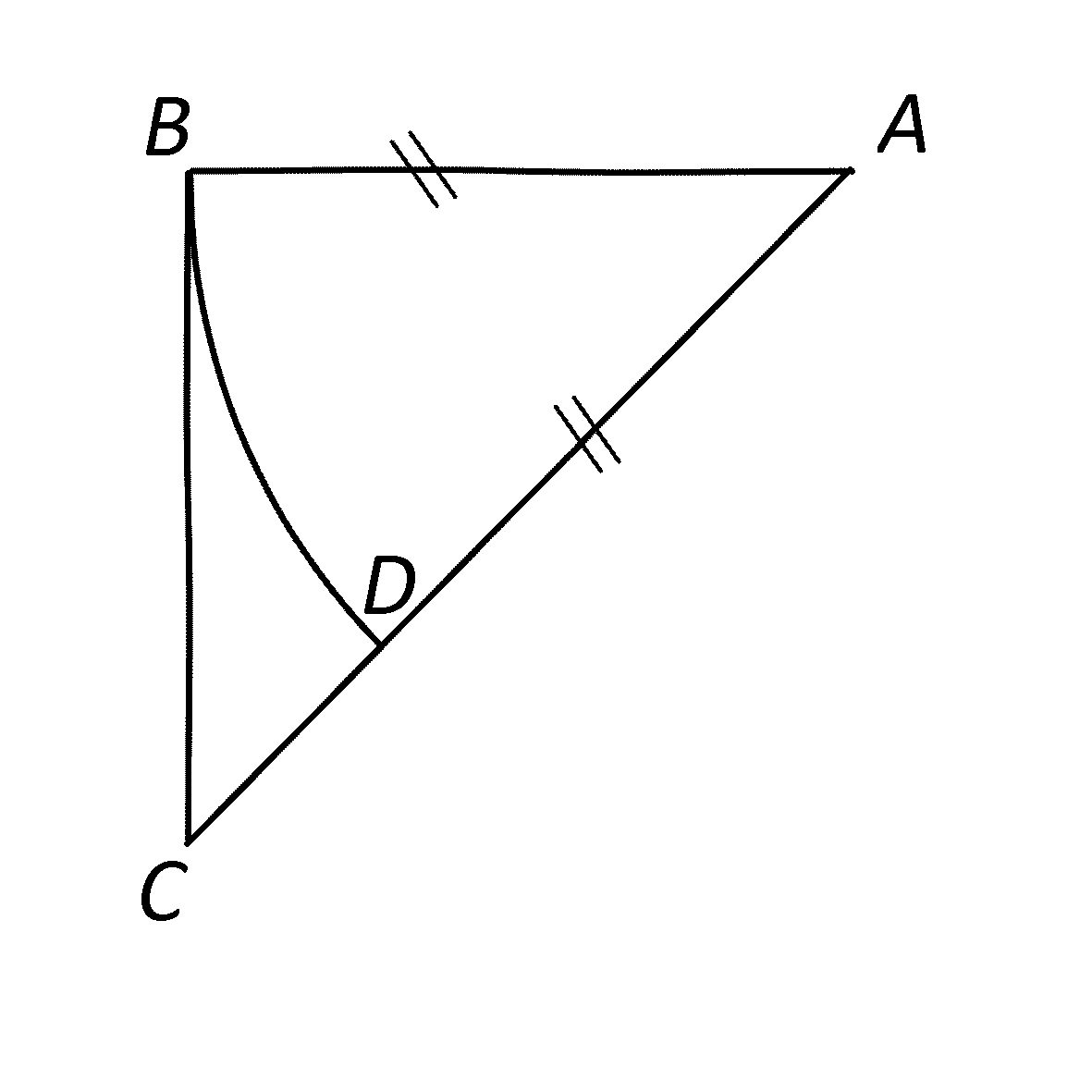
直角3角形の長辺 \(AC\) 上に、\(AB=AD\) となる点 \(D\) を選ぶ。このとき、\(AC=AD+DC=AB+DC\) なので、さっきの式から、
$$ \sqrt{2} = \frac{AC}{AB}= \frac{AB+DC}{AB} = 1 +\frac{DC}{AB}, $$
となる。したがって、\(\sqrt{2}\) が分数なら、\(DC/AB\) も分数のはずだ。

次に、\(D\) を通って \(AC\) と直交する線を引き、辺 \(BC\) と交わる点を\(E\)とする。このとき、\(\angle DCE\) が45度なので、\(DCE\) は直角3角形になり、\(DC=DE\) だ。また、また、3角形 \(ADE\) と \(ABE\) は合同なので、\(DE=BE\)。つまり、\(DC=BE\) なので、
$$ AB=BC=BE+EC=DC+EC,$$
と書くことができる。これをさっきの \(\sqrt{2}\) の式に代入すると、
$$ \sqrt{2} = 1 +\frac{DC}{AB}=1 + \frac{DC}{DC+EC}= 1+\cfrac{1}{1+\cfrac{EC}{DC}}, $$
となる。
ところが、さっき示したように、\(CEF\) は直角3角形なので、
$$ \frac{EC}{DC} = \sqrt{2}.$$
したがって、
$$ \sqrt{2}= 1+\frac{1}{1+\sqrt{2}}. $$
これは、本文の7節で、\(\sqrt{2}\) の連分数表示を導いたときに使った式に他ならない。これを繰り返すと、連分数表示が無限に続くので、\(\sqrt{2}\) は自然数の比では表せないことがわかった。
連分数が無限に続く様子は、下の図のように幾何学的に表すことができる。