第7話 補遺
① 2次関数の積分
2次関数 \(y = x^2\) の \(x=0\) から \(x=a\) までの面積を計算しよう。このとき、図形C\(_n\) は底辺 \(\epsilon=a/n\)、高さが \(\epsilon^2, (2\epsilon)^2, \cdots \) の長方形の集まりなので、
\begin{align}(図形{\rm C}_nの面積) &= \epsilon^2 \times \epsilon +\cdots + (n \epsilon)^2 \times \epsilon \\& = \left( 1^2 + 2^2 + \cdots + n^2 \right) \times \epsilon^3 , \end{align}
となる。アルキメデスは、この \(( 1^2 + 2^2 + \cdots + n^2 )\) を
$$1^2 + 2^2 + \cdots + n^2 = \frac{1}{3} n^3 + \frac{1}{2} n^2 + \frac{1}{6} n , $$
と計算した。これが正しいことを、帰納法で証明しよう。
[証明はじめ]
まず、 \(n=1\) のときには、左辺は1で、右辺も \(1/3 + 1/2 + 1/6 = 1\) なので、確かに正しい。
次に、この公式が自然数 \(n\) のときに正しいと仮定すると、\(n+1\) のとき、
\begin{align}1^2 + 2^2 + \cdots +n^2+ (n+1)^2 & = \frac{1}{3} n^3 + \frac{1}{2} n^2 + \frac{1}{6} n +(n+1)^2 \\& = \frac{1}{3} (n+1)^3 + \frac{1}{2} (n+1)^2+ \frac{1}{6} (n+1) \ , \end{align}
となって正しい。帰納法によって、この公式がすべての自然数について成り立つことがわかった。
[証明おわり]
この公式を使うと、図形C\(_n\) の面積は、
\begin{align}(図形{\rm C}_nの面積) & = \left( \frac{1}{3} n^3 + \frac{1}{2} n^2 + \frac{1}{6} n \right) \times \epsilon^3 \\& = \left( \frac{1}{3} n^3 + \frac{1}{2} n^2 + \frac{1}{6} n \right) \times \left( \frac{a}{n}\right)^3 \\ & = \left( \frac{1}{3} + \frac{1}{2n} + \frac{1}{6n^2}\right) \times a^3 \ ,\end{align}
となる。そこで \(n\) を大きくしていくと、括弧の中の \(1/n\) や \(1/n^2\) の項はいくらでも小さくなり、無視できるようになるので、\(n\) が無限大の極限では面積は \(a^3/3\) になる。これがアルキメデスが計算した放物線の下の面積だ。積分の表式を使うと
$$ \int_0^a x^2 dx = \frac{a^3}{3} \ , $$
と書ける。
② 指数関数の微分の補足
第8節で指数関数の微分を計算するのに使った公式、
$$ \lim_{\epsilon \rightarrow 0} \frac{e^{\epsilon}-1}{\epsilon} = 1 \ , $$
を証明しよう。
そのためには、\(\epsilon\) が小さいときに \(e^{\epsilon}\) がどんなものか知る必要がある。そこで役に立つのが、第6回「大きな数を恐れないということ 後編」の「資産運用の法則」で登場した自然対数の性質、
$$ \log_e \left( 1 + \epsilon \right) \fallingdotseq \epsilon \ , $$
だ。この式は \(\epsilon\) が小さいときだけ近似的に正しいので\(\fallingdotseq\) でつないでいる。一方、対数関数の定義から、
$$ \log_e e^\epsilon = \epsilon \ , $$
なので、この2つを比較すると、
$$ \log_e e^\epsilon \fallingdotseq \log_e \left( 1 + \epsilon\right) \ . $$
この式から対数をはらうと、
$$ e^\epsilon \fallingdotseq 1+ \epsilon \ , $$
となる。つまり、\(\epsilon\) が小さくなっていくと、\((e^{\epsilon}-1)\) は\(\epsilon\) に等しくなっていく。だから、
$$ \lim_{\epsilon \rightarrow 0} \frac{e^{\epsilon} - 1}{\epsilon} = 1 \ . $$
これが証明したいことだった。
③ 指数関数を直接積分する
区間 \(a \leq x \leq b\) を \(n\) 等分して \(\epsilon = (b-a)/n\) とすると、積分の定義から、
\begin{align}\int_a^b e^x dx &=\lim_{\epsilon \rightarrow 0} \big( e^{a+\epsilon} + \cdots + e^{a+ n \epsilon} \big) \times \epsilon \\ &=\lim_{\epsilon \rightarrow 0}e^{a}\times \big( e^{\epsilon} + \cdots + e^{n \epsilon} \big) \times \epsilon \ , \end{align}
となる。この計算をするには「等比級数の和」の公式、
$$e^\epsilon + e^{2\epsilon} + \cdots + e^{n\epsilon} = \frac{e^{(n+1)\epsilon}-e^\epsilon}{e^\epsilon-1} \ , $$
が必要になる。ここで、\(n\epsilon = b-a\) だということを思い出すと、
\begin{align}\int_a^b e^x dx &= \lim_{\epsilon\rightarrow 0} e^a \times \frac{e^{b-a +\epsilon}-e^\epsilon}{e^\epsilon - 1}\times \epsilon \\ &= \lim_{\epsilon\rightarrow 0} (e^{b+\epsilon} - e^{a+\epsilon})\times \frac{\epsilon}{e^\epsilon - 1} \ , \end{align}
となる。この右辺に、指数関数の微分の計算で登場した、
$$ \lim_{\epsilon\rightarrow 0} \frac{e^\epsilon - 1}{\epsilon} = 1 \ , $$
と、\(\epsilon \rightarrow 0\) で \(e^{a+\epsilon}\rightarrow e^a\)、\(e^{b+\epsilon}\rightarrow e^b\) となることを使うと、
$$ \int_a^b e^x dx=e^b-e^a \ ,$$
となって、指数関数の積分の公式が再確認できた。
指数関数の微分と積分を比較すると、微分の方は
$$ \lim_{\epsilon\rightarrow 0} \frac{e^\epsilon - 1}{\epsilon} = 1 \ , $$
を使えばすぐに計算できるが、積分の方は等比級数の和を計算するという手間がかかっている。これが三角関数になると、微分と積分の難易度の違いはさらに大きくなる。
④ 3角関数の微分と積分
まず、3角関数について復習しておこう。3角関数を \(\sin \theta\)、\(\cos \theta\)、\(\tan \theta\) と書くときの \(\theta\) は、角度を「ラジアン」という単位で測ったものだ。これは、円を一周するときの角度を、360度ではなく、\(2\pi\) とする単位だ。ラジアンでは直角は \(\pi/2\) になる。また、半径1の円周は \(2\pi\) だから、円を \(theta\) ラジアンで切り取ったときの円弧の長さはちょうど \(\theta\) になる。
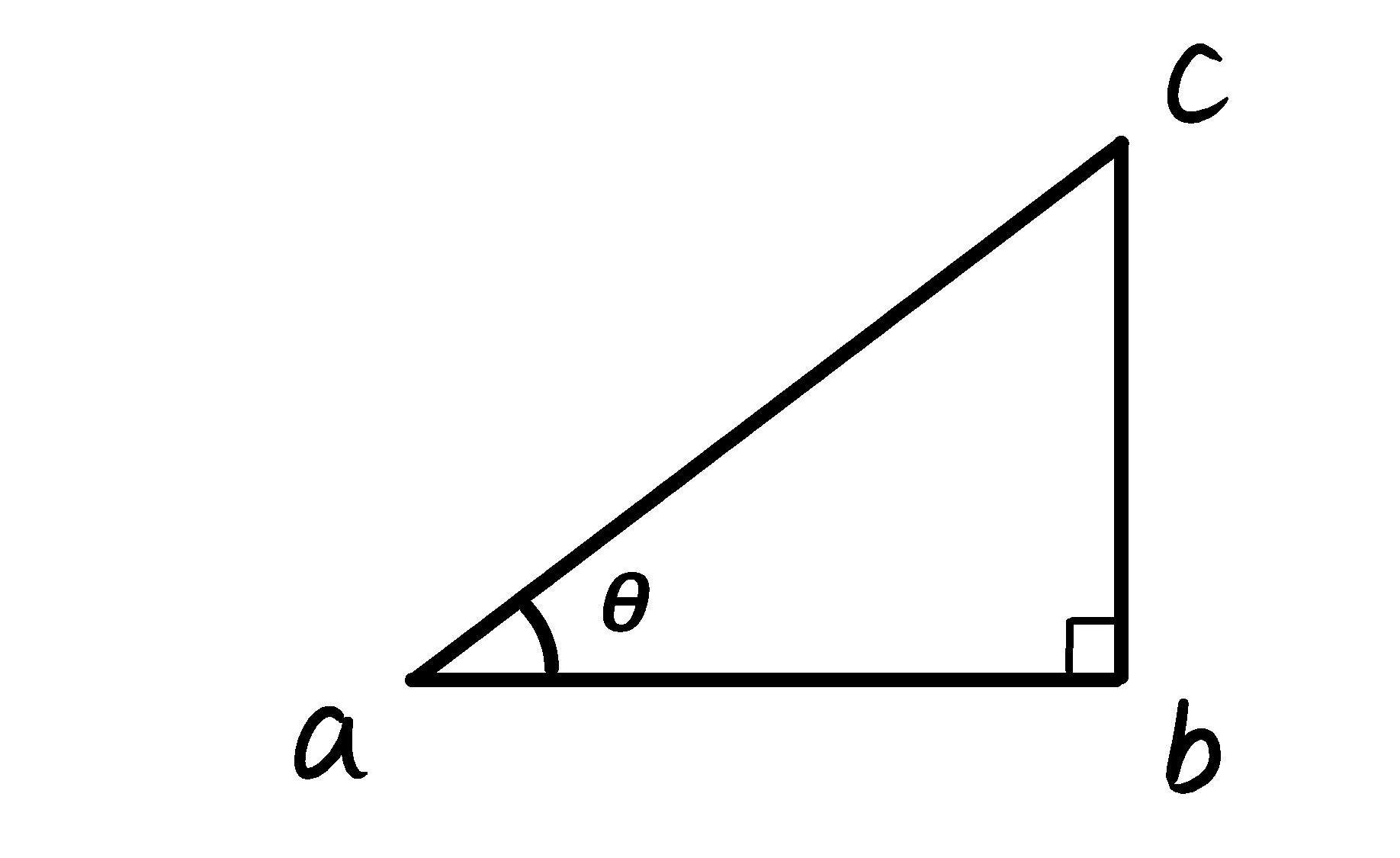
3角関数を定義するには、上の図のように、頂点 \(a\)、\(b\)、\(c\) の直角3角形を考え、頂点 (a\) の角度が \(\theta\)、頂点 \(b\) は直角とする。このとき、
☆ \(\sin x\) は高さ \(\overline{bc}\) と斜辺 \(\overline{ac}\) の比、
$$ \sin \theta = \frac{\overline{bc}}{\overline{ac}}\ , $$
☆ \(\cos x\) は底辺と斜辺の比、
$$ \cos \theta = \frac{\overline{ab}}{\overline{ac}} \ , $$
☆ \(\tan x\) は高さと底辺の比、
$$ \tan \theta = \frac{\overline{bc}}{\overline{ab}} \ , $$
だ。また、\(\sin \theta\) と \(\cos \theta\) の比を考えると、斜辺がキャンセルされて、高さと底辺の比、つまり、\(\tan \theta\) になる。
$$ \frac{\sin \theta}{\cos \theta} = \tan \theta \ . $$
3角関数を習ったときに、どうして角度をラジアンで測るのか疑問に思ったことはないかな。そのご利益は、微積分を勉強して初めてわかる。3角関数の微分や積分で使う公式に、こんなものがある。
$$ \lim_{\theta\rightarrow 0} \frac{\sin \theta}{\theta} = 1 \ . $$
もし、一周360度の角度で3角関数を定義すると、右辺は1ではなく \(2\pi/360=\pi/180\) となってしまう。そうすると、微積分の公式に \(\pi\) やら180やらが現れて、式がゴチャゴチャしてくる。角度を測るのにラジアンを使う理由は、微積分の計算をやりやすくする
ためなんだ。
この公式は、三角関数の微積分の基本なので、証明しておこう。そこで使うのは、またしても「はさみうち」だ。

[証明はじめ]
上の図のように半径1の円を描いて、角度 \(\theta\) で切り取る。そのときにできる扇形の面積は、円全体の面積の \(\theta/2\pi\)。半径1の円の面積は \(\pi\) なので、扇形の面積は \(\theta/2\) になる。
次に、図の3角形 \(abc\) を考える。3角形 \(abc\)は、斜辺が1だから高さは \(\sin \theta\)。底辺は1なので、面積は \(\sin \theta/2\) になる。この3角形は、円から切り取った扇形に含まれているので、3角形 \(abc\) と扇形の面積を比べると、
$$ \frac{\sin \theta}{2} < \frac{\theta}{2} \ , $$
つまり、
$$ \frac{\sin \theta}{\theta} < 1 \ , $$
となる。
一方、3角形 \(abd\) は、底辺1で高さは \(\tan \theta\) なので、面積は \(\tan \theta/2\) だ。この3角形は、面積 \(\theta/2\) の扇形を含んでいるので、
$$\frac{\theta}{2} < \frac{\tan \theta}{2} \ . $$
ここで、\(\tan \theta = \sin\theta / \cos\theta\) を思い出すと、
$$ \cos\theta < \frac{\sin\theta}{\theta} \ , $$
となる。
上の2つの段落の不等式を組み合わせると、\(\sin\theta /\theta\) のはさみうちができる。
$$ \cos \theta <\frac{\sin \theta}{\theta} < 1 \ .$$
\(\cos \theta\) は直角3角形の底辺と斜辺の比だから、斜辺の角度\(\theta\) が小さくなると、斜辺と底辺の長さは等しくなり、\(\cos\theta \rightarrow 1 \) となる。つまり、\(\theta \rightarrow 0\) の極限では、\(\sin \theta / \theta\) は、右からも左からも1ではさまれるので、
$$ \lim_{\theta \rightarrow 0} \frac{\sin \theta}{\theta} = 1 \ .$$
となる。
[証明おわり]
この式は、\(\epsilon\) が小さいときに、
$$ \sin \epsilon \fallingdotseq \epsilon \ , $$
と表すこともできる。
では、準備ができたので、三角関数の微分を計算しよう。
微分の定義から、
\begin{align}\frac{d}{d\theta} \sin\theta &=\lim_{\theta'\rightarrow \theta}\frac{\sin\theta' - \sin\theta}{\theta'-\theta} \\ &= \lim_{\epsilon \rightarrow 0} \frac{\sin (\theta+\epsilon) - \sin\theta}{\epsilon} \ \end{align}
ここで、三角関数の加法定理を使う。加法定理自身については、この連載の第8話で、複素数についての話をするときに詳しく説明することにして、ここではまず、公式を眺めてみよう。
$$\sin(\theta_1 +\theta_2) = \cos \theta_1 \times \sin \theta_2 + \sin \theta_1 \times \cos \theta_2 \ . $$
これは、左辺にある \((x+y)\) の三角関数を、右辺のように \(x\) と \(y\) の三角関数の積の和で表す式だ。
この加法定理を使うと、
$$\sin (\theta+\epsilon) - \sin \theta = \cos \theta \times \sin +\sin \theta \times \big( \cos \epsilon -1 \big) \ . $$
右辺第1項には \(\sin \epsilon\) があるけれど、これはさっき示したように\(\epsilon\)で近似することができる。また、右辺第2項の \((\cos \epsilon - 1)\) は、\(-\frac{1}{2}\epsilon^2\) で近似できる。これは、ピタゴラスの定理 \((\sin \epsilon)^2 + (\cos \epsilon)^2 = 1\) と \(\sin \epsilon \fallingdotseq \epsilon\)を 使えば証明できる。
[証明はじめ]
\((\sin \epsilon)^2 + (\cos \epsilon)^2 = 1\) で、\((\cos \epsilon)^2\) を右辺に移項して、因数分解すると、
$$(\sin \epsilon)^2 = 1 - (\cos \epsilon)^2 = (1 + \cos \epsilon)\times (1- \cos \epsilon),$$
となる。\(\epsilon\) が小さいときには、\(\cos \epsilon\) はほぼ1に等しいから、\(1 + \cos \epsilon \fallingdotseq \ 2\) と書くと、右辺は、
$$ (1 + \cos \epsilon)\times (1- \cos \epsilon)\fallingdotseq 2 (1 - \cos \epsilon).$$
これが、左辺の \((\sin \epsilon)^2 \fallingdotseq \epsilon^2\) に等しいというのだから、
$$\epsilon^2 \fallingdotseq 2( 1 - \cos \epsilon),$$
つまり、
$$\cos \epsilon - 1\fallingdotseq -\frac{1}{2}\epsilon^2,$$
となる。
[証明おわり]
だから、
$$\sin (\theta+\epsilon) - \sin x \fallingdotseq \cos \theta \times \epsilon-\frac{1}{2} \sin \theta \times \epsilon^2 \ .$$
これを \(\epsilon\) で割ると、右辺第2項は \(-\frac{1}{2} \sin \theta\times \epsilon\) となるので、\(\epsilon \rightarrow 0\) の極限ではゼロになる。ゼロにならずに残るのは第1項だけ。つまり、
\begin{align}\frac{d}{d\theta} \sin x &= \lim_{\epsilon \rightarrow 0} \frac{\sin (\theta+\epsilon) - \sin\theta}{\epsilon}\\ &= \lim_{\epsilon \rightarrow 0}\left( \cos\theta - \frac{1}{2} \sin\theta \times \epsilon \right) \\ & =\cos x \ .\end{align}
で、\(\sin \theta\) の微分は \(\cos\theta \) になる。同じく、\(\cos \) についての加法定理、
$$\cos (\theta + \epsilon) =\cos \epsilon \times \cos \theta - \sin \epsilon \times \sin \theta \ , $$
を使うと、
\begin{align} \frac{d}{d\theta} \cos x &= \lim_{\epsilon \rightarrow 0} \frac{\cos (\theta+\epsilon) - \cos\theta}{\epsilon} \\ &= - \sin \theta \ \end{align}
となる。
微分がわかったので、「微積分法の基本定理」を使えば積分もできる。たとえば、
\begin{align}\int_a^b \sin\theta \ d\theta & = \int_a^b \left( - \frac{d}{d\theta} \cos\theta\right) d\theta \\&= - \cos b + \cos a \ , \end{align}
となる。
3角関数の積分を定義に戻って計算するのは簡単ではない。積分を定義から計算するためには、べき関数のときには、
$$1^k + 2^k + \cdots + n^k = \frac{n^{k+1}}{k+1} + \frac{n^k}{2} + \cdots \ , $$
指数関数のときには、
$$e^\epsilon + e^{2\epsilon} + \cdots + e^{n\epsilon}= \frac{e^{(n+1)\epsilon} - e^\epsilon}{e^\epsilon - 1} \ , $$
を使った。同じことを3角関数でしようとすると、
$$ \sin(\theta+\epsilon) + \cdots + \sin(\theta+n\epsilon) \ , $$
を計算しなければならなくなる。これは、第8話で紹介する「オイラーの公式」を使うとすぐにできるが、それを知らずに3角関数の加法定理を何度も使って計算しようとすると大変だ。


