第3話 補遺
① 風力発電はどのくらい実用的か
本書では、フェルミ推定の例として、最近の大気中の二酸化炭素濃度の増加は、人類の活動による可能性が高いことを示した。二酸化炭素の排出による気候への影響は心配だし、その原因となる化石燃料はそのうち枯渇してしまうだろう。原子力発電の安全性には不安があるし、使用済み核燃料をどのように保存するかの問題も解決していない。人類がこれから数千年以上にわたって繁栄するためには、安全で再生可能なエネルギー源の開発が必要だ。
代替エネルギー源として、風力発電がある。そこで、風力発電では、どのくらい電気を作ることができるか考えてみよう。
僕らは、ある程度強い風が吹いていても、それに逆らって歩くことができる。ということは、僕らの体に受ける風の強さは、僕らのエネルギー出力よりもずっと弱いということだ。だから、長さが1メートル程度の羽根を使ったのでは、1人当たりの消費エネルギーの数十分の1程度、電力にして数ワットしか生産できない。
もちろん羽根を大きくすれば、エネルギー出力は増えるけれど、大きな羽根を回すには大きな敷地がいる。僕らの今の見積もりによると、風車のように羽根をグルグル回すタイプの風力発電では、人間1人分の出力を出すには、数十平方メートルが必要だ。
本書では、現代人の消費エネルギーは、食事から得るエネルギーの50倍、100,000キロカロリーと推定した。日本にはおよそ1億人の人がいるので、全体の消費エネルギーは50億倍。風力発電で人間1人分の出力を出すには数十平方メートル必要だとすると、日本の消費エネルギーをすべて風力発電でまかなうには、\(10^{11}\) 平方メートル程度の敷地が必要になる。
これを日本国土の面積と比べてみよう。東京と大阪間はおよそ500キロだ。これは日本列島の長さの数分の1だけれど、日本は細長いから、全体の面積はおよそ \(500 \times 500 = 2.5 \times 10^5\) 平方キロ、つまり \(2.5 \times 10^{11}\) 平方メートルと見積もられる(この計算をしてから、国土地理院のウェブページを見てみたら、\(3.8\times 10^{11}\) 平方メートルだった)。これは、風力発電に必要な面積と同じくらいだ。
風力発電で日本のエネルギー需要のすべてをまかなおうとすると、国土の大部分が必要になるとわかる。たとえば、海上に設置するなども考えられるし、またもっと効率よくエネルギーを生産するデザインがあるかもしれない。しかし、風力発電だけに頼るのは無理そうだ。
僕らが持続して使えるエネルギー源は、究極的には地中の原子核エネルギーと太陽からの光しかない。風力エネルギーも、太陽のエネルギーから派生したものだ。もし太陽光の大部分を利用可能なエネルギーに変換できたら、日本はエネルギーの自給ができるようになるだろうか。
日本に降り注ぐ太陽の光は、1平方メートル当たり人間2、3人分、電力にして200から300ワットに相当するそうだ。もし、この大部分をエネルギーに変換できれば、風力発電の数十倍の効率になる。そうなれば、日本の国土の数十分の1の面積で、日本の消費エネルギーがすべて生産できる。太陽光を利用可能なエネルギーに変換する方法の開発は、人類の将来にとって重要だと思う。
僕の所属するカリフォルニア工科大学では、2010年から人工光合成の研究所を立ち上げ、太陽からの光だけで、水と二酸化炭素から利用可能な燃料を生産する技術の開発に取り組んでいる。植物が10億年以上前からやっていることを、より効率的に行なおうという試みだ。
② \(\log_e ( 1 + \epsilon) \fallingdotseq \epsilon\)の証明
まず、\(\log_e e^x=x\) という対数の定義を思い出そう。ここで、\(x=1\) とすると、\(e = e^1\) なので、
$$\log_e e = \log_e e^1=1 ,$$
となる。一方、\(n\) が大きいときに、\(e\fallingdotseq (1 + 1/n)^n\) だから、この式は、
$$\log_e \left(1+\frac{1}{n}\right)^n \fallingdotseq 1 \ , $$
と書くこともできる。そこで、\(\log_e (1 + 1/n )^n = n \times \log_e(1+1/n)\) を使うと、
$$ n \times \log_e \left(1 + \frac{1}{n}\right) \fallingdotseq1.$$
この両辺を \(n\) で割れば、
$$ \log_e \left(1 + \frac{1}{n}\right)\fallingdotseq \frac{1}{n},$$
となる。\(n\) は大きな数だから、\(1/n\) は小さな数。これから、小さな数\(\epsilon\) については、
$$ \log_e ( 1 + \epsilon) \fallingdotseq \epsilon \ ,$$
という簡単な式が近似的に成り立つことがわかる。
③ 運命の人を射止める
ネイピアの数 \(e\) は、複利計算だけでなく、いろいろなところに現れる。
恋人の候補が \(N\) 人いて、その中で自分が一番気に入った人を選びたいとする。恋人候補が一度に登場してくれれば、全員を比べて1位の人を選ぶのは簡単だが、そうではなくて、1人ずつ順番に面接するとしよう。候補は \(N\) 人であることはわかっているが、どんな順番で現れるかはわからない。断ると、次の人が登場する。前の人の方がよかったとなっても、戻ることはできない。いったん断った人とは、二度と会うことはない。
話を簡単にするために、君は \(N\) 人の候補を比較するときには、迷わずに1位、2位、…、\(N\) 位とランク付けすることができて、同点はないものとする。面接の目的は1番好きな人を選ぶことで、2位や3位の人を選んでも意味がないとしよう。
たとえば、一番最初に来た人を選んだ場合、その人が1位である確率は \(1/N\) だ。この方法では、\(N\) が大きくなると、運命の人に出会える確率は小さくなる。ところが、\(N\) がいくら大きくなっても、0.368程度の確率で1位の人を選べる方法がある。それを説明しよう。
恋人候補と面接をするときに、「観察モード」と「本気モード」に分けて対応することにする。最初の \((m-1)\) 人とは、ただ会ってみるだけで、全員断ることにする。これが観察モードだ。そして、\(m\) 人目になったところで、本気モードのスイッチを入れる。本気モードでは、これまでに会ったどの人よりも気に入った人なら、その人を選ぶことにする。この戦略を取ったときに、1位の人を選べる確率を \(D(m, N)\) と書くことにしよう。\(D\) はDestiny (運命)の頭文字。\(N\) 人の候補がいるときに、\(m\) 人目から本気モードになって、運命の人を射止める確率なので、\((m,N)\) と書き添えた。
候補が2人の場合、つまり \(N=2\) のときには、1位の人は最初に現れるか2番目に現れるかしかないから、1位の人を選べる確率は、\(m=1\) でも \(2\) でも \(1/2\) だ。
候補が3人になると、戦略によって確率が変わる。3人の候補が現れる順番は、ランキングをつけて書くと、
\begin{align}&[{\bf 1},2,3]\ , \ [{\bf 1},3,2]\ , \ [2,{\bf 1},3]\ , \\ & [3,{\bf 1},2]\ , \ [2,3,{\bf 1}]\ , \ [3,2,{\bf 1}]\ ,\end{align}
の6通りある。わかりやすいように、1位をオレンジ色で書いておいた。この6通りの中で、最初に1位の人が現れるのは \([{\bf 1},2,3]\) と \([{\bf 1},3,2]\) の2通りなので、最初の人を選んで成功する確率は\( 2/6=1/3\) となる。
2人目から本気モードになると、\([2,{\bf 1},3]、 [3,{\bf 1},2]、 [2,3,{\bf 1}]\) の3通りの場合に成功する。\([3,2,{\bf 1}]\) の順番のときにも、本気モードになった後で1位の候補が現れるが、2人目に2位の候補が登場して、そちらを選んでしまう。1位の候補には会えないんだ。だから、2人目に本気モードになる戦略で成功する確率は、\( 3/6=1/2\) となる。
3人目まで待って、最後の人を選んだときにうまくいくのは、\([2,3,{\bf 1}]\) か \([3,2,{\bf 1}]\) の場合で、確率は \(1/3\)。
まとめると、
$$D(1,3) = \frac{1}{3} \ ,\qquad D(2,3) = \frac{1}{2} \ , \qquad D(3,3) = \frac{1}{3} ,$$
で、1番の人を選ぶためには、2人目の候補から本気モードになるといいことがわかる。
このように場合分けをして計算すると、候補が \(N\) 人いるときに、\(m\) 人目から本気モードになって、1番好きな人を射止められる確率は、
$$D(m, N ) = \frac{1}{N} +\frac{m-1}{N} \left( \frac{1}{m} + \cdots + \frac{1}{N-1} \right), $$
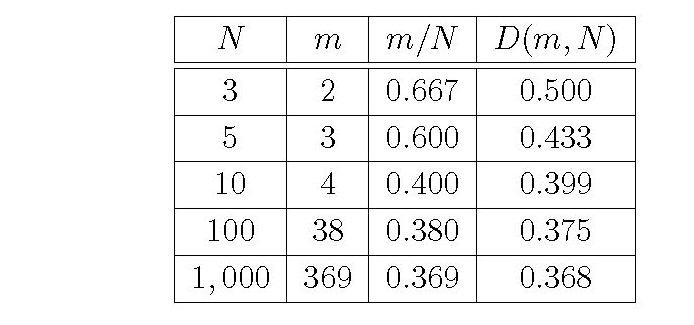
となる。この公式を使うと、候補の数 \(N\) がわかっているときに、何番目の候補から本気モードになればよいかが計算できる。いくつかの \(N\) について、確率 \(D(m,N)\) を最大にする \(m\) と、そのときの \(D(m,N)\) の値を表にしてみよう。
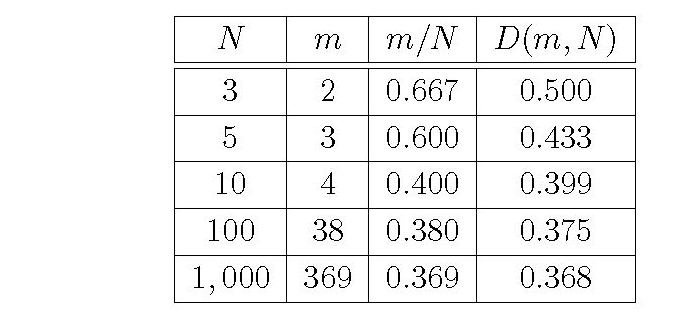
候補者が \(N\) 人いて、その中でランダムに1人を選んだときに、1位の人を選ぶ確率は \(1/N\)。この確率は、\(N\) が大きくなると、どんどん小さくなる。ところが、観察モードと本気モードを組み合わせた戦略を使うと、いくら \(N\) が大きくなっても、確率が下がらないようにできる。たとえば、\(N=1000\)のときには、ランダムに選んで成功する確率は \(1/1000\) だが、\(m=369\) で本気モードになれば、\(0.368\) の確率で運命の人を射止めることができる。この \(0.368\) は、ネイピア数の逆数 \(1/e=0.3678794\cdots\) に近い。\(N\) をもっと大きくしていくと、確率 \(D(m,N)\) を最大にする \(m\) は、\(m = N/e\) に近づいていく。つまり、全体の36.8パーセントぐらいの候補を眺めてから、本気モードになれということだ。そして、そのときの確率も \(D(m, N) = 1/e\) に近づく。どんなに\(N\)が大きくなっても、\(m = N/e\) 番目から本気モードになる戦略をとれば、\(1/e\) の確率で成功するんだ。
天文学者ケプラーが1613年にストラーデンドルフ男爵に書いた手紙によると、彼は最初の妻を亡くしたときに、2年がかりで慎重に再婚相手を選んだ(最初の結婚は幸福なものではなかったらしい)。11人の候補と順番にお見合いをすることにしたが、5人目の候補に求婚したそうだ。\(N=11\) のときには、確率 \(D(m, N=11)\) は \(m=5\) で最大になるので、ケプラーはこの戦略を知っていたのかもしれない。
なぜこんなところにネイピア数 \(e\) が登場するか。これを説明するために、
$$D(m, N ) =\frac{1}{N} + \frac{m-1}{N} \left( \frac{1}{m} + \cdots + \frac{1}{N-1} \right) \ , $$
を最大にする \(m\) を求める。まず、\(m\) も \(N\) も大きいときには、この確率の式が、
$$ D(m, N) \fallingdotseq \frac{m}{N} \log_e \left(\frac{N}{m} \right) \ ,$$
と書けることを示そう。
【以下の説明は、微分と積分を使うともっと簡明になるけれど、第3話ではまだ微積分を説明していないので、少し長い説明になっている。微積を知っている人は、それを使った説明を考えてみよう。】
確率 \(D(m,N)\) の公式の中には、\(1/m\) から \(1/(N-1)\) までの和が含まれているが、\(m\) も \(N\) も大きいときには、対数を使って、
$$\frac{1}{m} + \cdots + \frac{1}{N-1}\fallingdotseq \log_e \left( \frac{N}{m} \right)\ , $$
と書くことができる。これを示すために、この和を、
$$f(m , N )= \frac{1}{m} + \frac{1}{m+1} + \cdots + \frac{1}{N-1} \ , $$
と書いてみる。ここで、\(m\) を \(m \rightarrow m+1\) と置き換えると、
$$f(m+1, N) = \frac{1}{m+1} + \cdots + \frac{1}{N-1} \ , $$
なので、\(f(m, N)\) と \(f(m+1, N)\) の差を計算すると、右辺の \(1/m\) 以外は相殺されて、
$$ f(m, N) - f(m+1, N) = \frac{1}{m} \ ,$$
という式が成り立つ。
一方、対数については、第5節で、\(m\) が大きいときに、
$$ \log_e \left( 1 + \frac{1}{m} \right) \fallingdotseq \frac{1}{m} \ , $$
が成り立つという話をした。対数には、\(\log_e X - \log_e Y = \log_e (X/Y)\) という性質があるから、
\begin{align}\log_e (m +1) - \log_e m \\ &= \log_e \left( \frac{m+1}{m} \right) \\ &= \log_e \left( 1 + \frac{1}{m} \right) \ . \end{align}
つまり、
$$ \log_e (m +1) - \log_e m \fallingdotseq \frac{1}{m} \ , $$
となる。一方、\(f(m, N) - f(m+1, N) \) も \(1/m\) に等しいので、\(1/m\) に等しいもの同士は等しいということで、
$$f(m, N) - f(m+1, N)\fallingdotseq \log_e (m +1) - \log_e m \ , $$
と書くことができる。この式で、\(f(m+1, N)\) を右辺に、\(\log_e m\) を左辺に移項すれば、
$$f(m, N) + \log_e m \fallingdotseq f(m+1, N) + \log_e (m+1) \ , $$
となる。
この式は何を意味しているのだろうか。左辺は \(f(m, N) + \log_e m\) で、右辺は同じ組み合わせで \(m \rightarrow m+1\) と置き換えたものだ。自然数 \(m\) の関数で、\(m \rightarrow m+1\) 置き換えても値が変わらないということは、\(f(m, N) + \log_e m \) という組み合わせは \(m\) によらないということだ。
では、その値は何だろうか。\(m\) が何であっても値は同じというのなら、たとえば、\(m=N-1\) としてもいいはずだ。もともと、\(f(m, N)\) は、\(1/m + \cdots + 1/(N-1)\) という和だったから、\(m=N-1\) とすると、\(f(m=N-1, N) = 1/(N-1)\) となる。ならば、
\begin{align}f(m , N) + \log_e m&\fallingdotseq f(N-1, N) + \log_e (N-1) \\ &= \frac{1}{N-1} + \log_e(N-1) \ . \end{align}
\(N\) が大きければ、右辺の \(1/(N-1)\) は小さくて無視できるし、\(\log_e(N-1)\) は \(\log_e N\) で近似できる(なぜなら、その差 \(\log_e (N-1) - \log_e N\) は \(\log_e (1 - 1/N)\)で、これは \(N\) が大きくなると \(-1/N\) と小さくなるから)。つまり、
$$f(m , N) + \log_e m \fallingdotseq \log_e N \ , $$
と書くことができる。ここで、\(\log_e m\) を右辺に移項すれば、
\begin{align} f(m, N) &\fallingdotseq \log_e N - \log_e m\\ & = \log_e \left( \frac{N}{m} \right) \ , \end{align}
となる。これで、\(m\) と \(N\) が大きいときには、
$$\frac{1}{m} + \cdots + \frac{1}{N-1} \fallingdotseq \log_e \left( \frac{N}{m} \right)\ , $$
となることが示された。
運命の人を射止められる確率は、
$$D(m, N ) = \frac{1}{N}+ \frac{m-1}{N} \left( \frac{1}{m} + \cdots + \frac{1}{N-1} \right) \ , $$
だったので、今の結果を使うと、\(m\) も \(N\) も大きいときには、
$$ D(m, N) \fallingdotseq \frac{m}{N} \log_e \left(\frac{N}{m} \right) \ ,$$
と書けることになる。
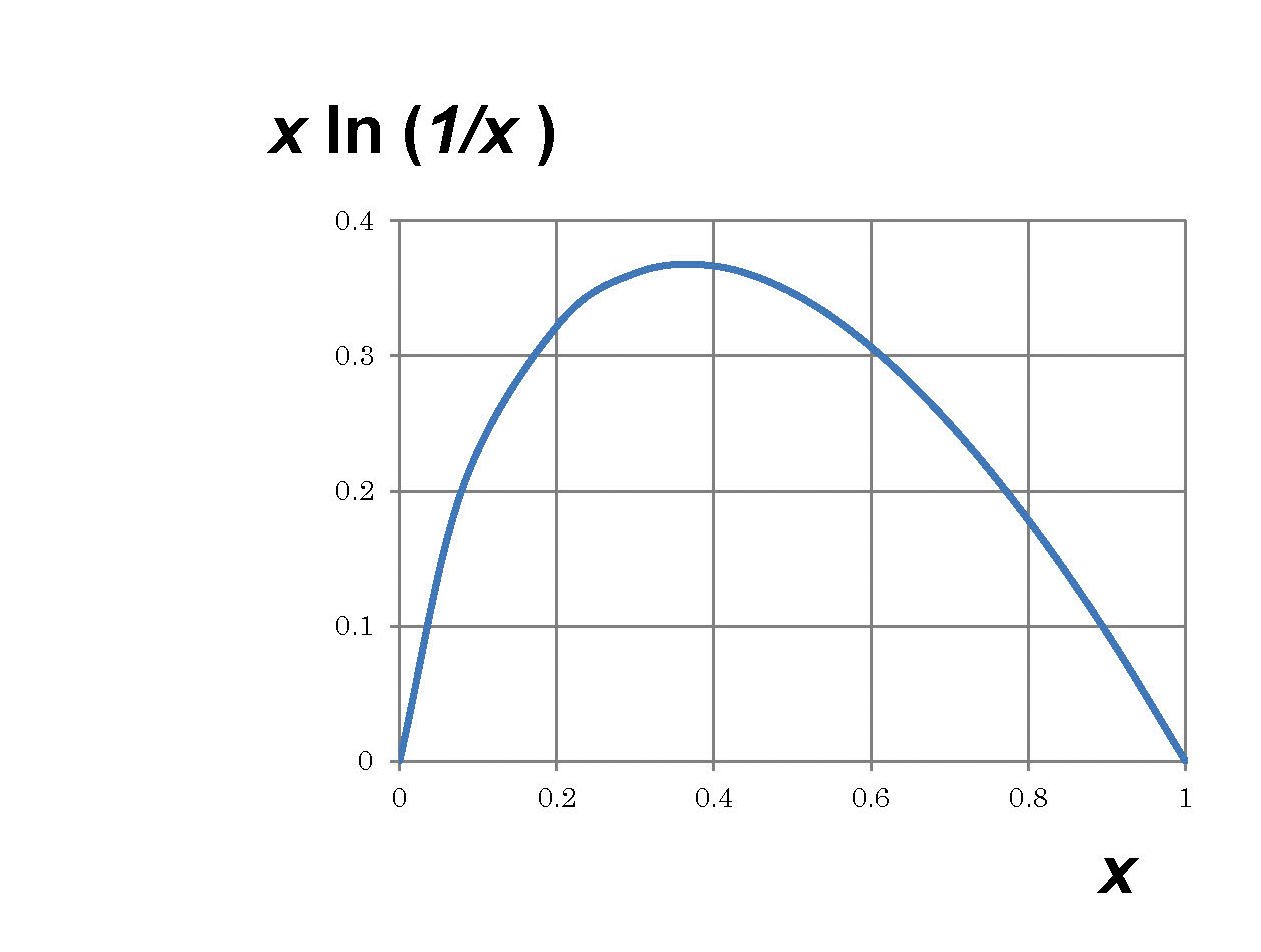
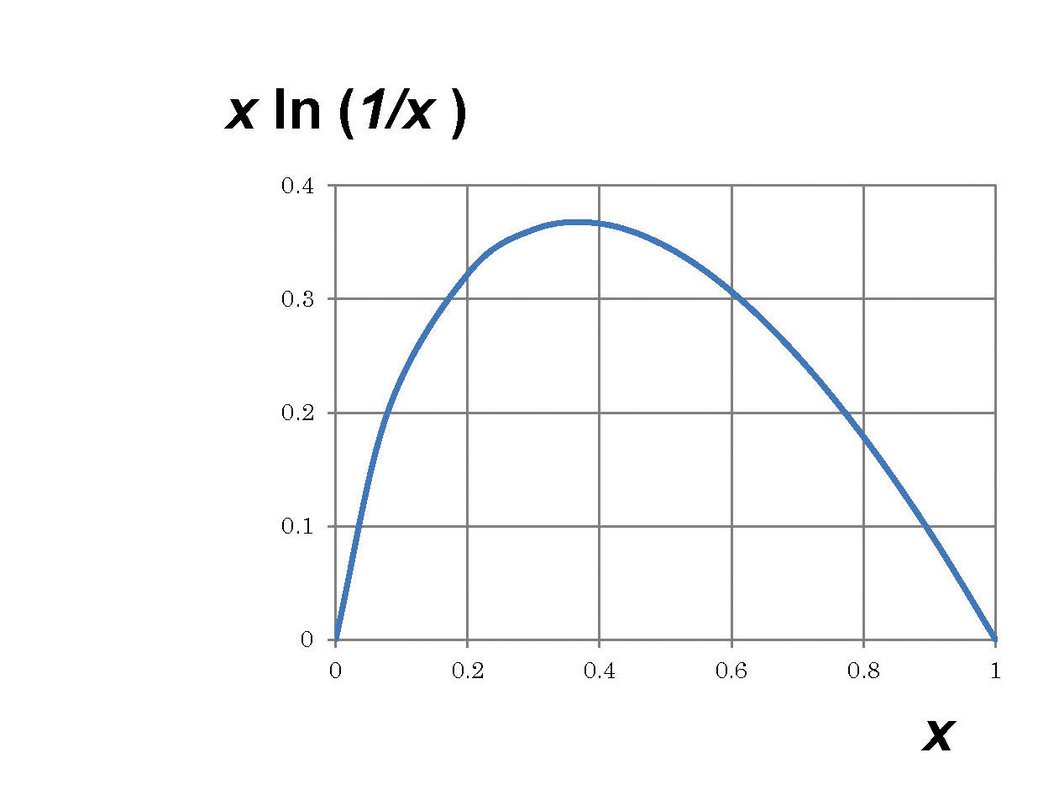
この式を使えば、運命の人を射止める確率 \(D(m, N))\) を最大にする \(m\) が求まる。上の \(y = x \log_e \left( \frac{1}{x}\right)\) のグラフを見てみよう(グラフには \(\log_e\) のことを \(\ln\) と書いてある)。およそ \(x = 0.37\) のところで、\(y\) が一番大きくなっていることがわかる。確率 \(D(m, N)\) の式と見比べると、\(x = m/N\) なので、\(m/N = 1/e\)、つまり、\(m = 0.37 \times N\) のときに確率が最大になることがわかる。
この0.37という数は、実はネイピア数を使うと、\(1/e\) となる。ピッタリ \(1/e\) になることは、次のようにすればわかる。
【以下の説明も、微分を使ったほうが簡明になる。】
上のグラフで \(x\) を0から順番に大きくしていくときの \(x \log_e \left( \frac{1}{x}\right)\) の様子を見ると、最初は大きくなっていって、\( x=0.37\) のあたりで最大になり、そのあとは小さくなっ ていく。つまり、\(m\) を大きくしていくと、確率 \(D(m, N) \fallingdotseq \frac{m}{N} \log_e \left(\frac{N}{m} \right)\) は、最初は増えていくが、\(m= 0.37 \times N\) のあたりで最大になって、その後は減っていく。確率が最大になっているあたりでは、\(m\) を\(m+1\) とずらしても、\(D(m, N)\) は増えも減りもしないだろう。
つまり、もし \(m\) が \(D(m, N)\) を最大にするのなら、\(D(m, N)\) はおよそ\(D(m+1, N)\) に等しいはずだ。そこで、そうなるような \(m\) を決めよう。
問題は、\(D(m, N) \fallingdotseq D(m+1, N)\)、つまり、
$$\frac{m}{N} \log_e \left(\frac{N}{m} \right) - \frac{m+1}{N} \log_e \left(\frac{N}{m+1} \right)\fallingdotseq 0 \ , $$
となる\(m\)は何かということだ。\(m\) が大きければ、
$$\log_e (m+1) - \log_e m \fallingdotseq \frac{1}{m} \ , $$
であることを使うと、この式は
$$ \log_e \left( \frac{N}{m+1} \right) \fallingdotseq 1 \ , $$
となる。僕らは、\(\log_e e = 1\) を知っているので、\(N/(m+1) = e\) と書くこともできる。\(N\) も \(m\) も大きいので、\(m\fallingdotseq N/e\) と近似してもいい。これが確率を最大にする \(m\) の値だ。
そのときには確率の値自身も、
\begin{align}D(m, N) &\fallingdotseq \frac{m}{N} \log_e \left(\frac{N}{m} \right)\\ &\fallingdotseq\frac{1}{e} \log_e e = \frac{1}{e} \ , \end{align}
となることがわかる(\(\log_e e =1\) であることを使った)。
\(N\)がいくら大きくなっても、\(m=N/e\)で本気モードに切り替える戦略を採用すれば、1位の人を選ぶ確率が \(1/e\) 程度になることがわ かった。ランダムに選んで1位の人を射止める確率が、\(1/N\) であることと比較すると、この戦略の効果がわかる。
この戦略には、しかし、リスクがある。最初の \((m-1)\) 人のなかに1位の人が紛れ込んでいると、運命の人を待っている間に、最後の候補になってしまうかもしれないからだ。そこで、目標を少し低く設定して、1位でなくてもいいから、選んだ候補のランクを平均して一番高くする方法はないかと考えてみる。
簡単な計算で、その場合には、\(m = \sqrt{N}\) 人目で本気モードになるのがよいことがわかる(\(\sqrt{N}\) が自然数でない場合には、一番近い自然数を選ぶ)。たとえば、100人候補がいる場合に、1位の人を選ぶためには38人目から本気モードになるのがよいけれど、候補のランクを平均的に一番高くなるようにするには、10人目から本気モードになるのがいい。
僕たちは、20年前にカリフォルニアに来て、最初に家を買うときにこの戦略を使った。毎週末に不動産屋に紹介された家を1軒ずつ見て、半年の間には買う家を決めたいとすると、全部で25軒程度の候補があることになる。候補を見たらすぐに決めないと他の人が買ってしまうから、今の話と似ている。そこで、\(\sqrt{25}=5\)なので、5軒目から本気モードで交渉を始めて、10軒目に見た家を買ったんだ。バークレイの丘からサンフランシスコが見渡せる素敵な家だったが、6年後にカリフォルニア工科大学に移籍したときに売ってしまった。
④ 対数と音階
音の高さは、周波数の対数で感じられているようだ。たとえば、音階の1オクターブ、「ドレミファソラシド」で、最初の「ド」と最後の「ド」では周波数が2倍になっている。1オクターブ上がるごとに、周波数が2倍になるんだ。
第2話で、「紀元前6世紀の偉大な数学者ピタゴラスは、2つの音の周波数の比が簡単な分数になるときに、その和音が美しく響くことを発見した」という話をした。1オクターブ離れた2つの「ド」の音の周波数は、\(1 : 2\) ととりわけ簡単な関係になっているので、1オクターブごとに音階が繰り返しているように感じるのだろう。
ピアノには、1オクターブの間に白鍵が7個、黒鍵が5個で、合計12個の鍵盤がある。最初の「ド」から1オクターブ上の「ド」に移動すると、周波数は2倍になる。鍵盤が12個あるということは、1オクターブを12の間隔に分割しているということだ。では、その分割の仕方はどのようにして決まっているのか。
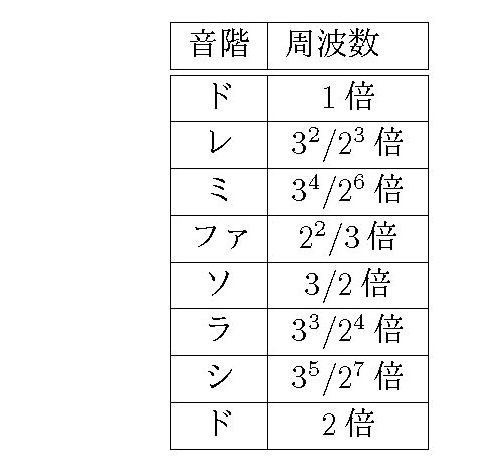
ピタゴラスが定めたと言い伝えられている「ピタゴラス音律」では、「レ」の音の周波数は「ド」の \(9/8=3^2/2^3\) 倍。その後は、
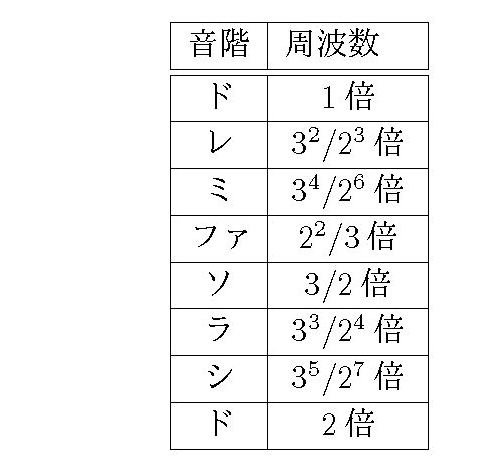
となっている。ピタゴラス音律の特徴は、\(2\) と \(3\) を基本にして、周波数を決めているところだ。たとえば、「ド」と「レ」の周波数の比は \(2^3 : 3^2\) となっている。「2つの音の周波数の比が簡単な分数になる」ように決めたのだが、分子や分母が大きな数になっているものがあるのが欠陥だ。たとえば、「ドミソ」は現在使われている音階ではきれいな和音になっているが、ピタゴラス音律では
「ド : ミ : ソ=\( 64:81:96 \)」。比率が簡単ではないので、不協和音になっている。
これを改善するために、15世紀に考え出されたのが「純正律(Just Intonation)」で、

となっている。これだと、「ド : ミ : ソ=\( 4:5:6\)」と、きれいな和音になっている。純正律では、どの音の組み合わせでも周波数の比が簡単な分数になっているので、和音が作りやすいという特徴がある。しかし、たとえば、「ド : レ=\( 8 : 9\)」なのに、「レ : ミ = \( 9 : 10\)」なので、転調をするとメロディが変わってしまうというのが問題だった。
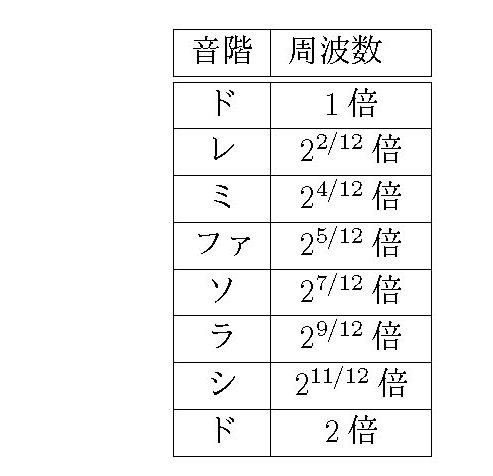
転調や移調が自由にできるためには、\( 12\) 個の鍵盤の隣り合う音の周波数の比が等しくなっていればよい。対数では割り算が引き算になるから、比が等しいということは、対数で計算したときに間隔が同じということだ。つまり、比を同じにするためには、1オクターブを対数で12等分すればよい。そこで、周波数を \( 2\) のべき乗で表して、指数が\( 1/12\) ずつ増えるようにする。
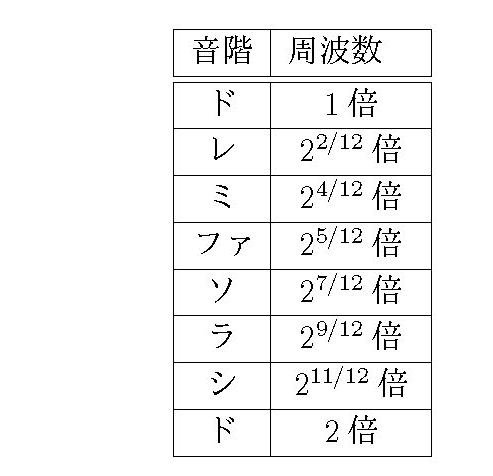
これが、現在標準的に使われている「平均律(Equal Temperament)」だ。「ミ」と「ファ」、「シ」と「ド」の間以外には黒鍵があるので、指数が\( 2/12\)ずつの間隔になっている。これだと、「ド : レ」も、「レ : ミ」も、\(1 : 2^{2/12}\) になっているので、転調をしてもメロディが変わらない。
一方、和音が美しく響くためには、2つの音の比が簡単な分数になっていなければいけない。1オクターブを対数で12等分すると、「ド : ソ=\( 1 : 2^{7/12}\)」となる。幸い、\(2^{7/12} =1.498\cdots\) と \(3/2=1.5\) とが非常に近いので、平均律では「ド」と「ソ」がうまくハモるようになっている。
⑤ べき乗の法則
自然界には、べき乗の法則がしばしば現れる。本書で解説したケプラーの法則はその有名な例だけれど、もう2つ例を紹介しよう。
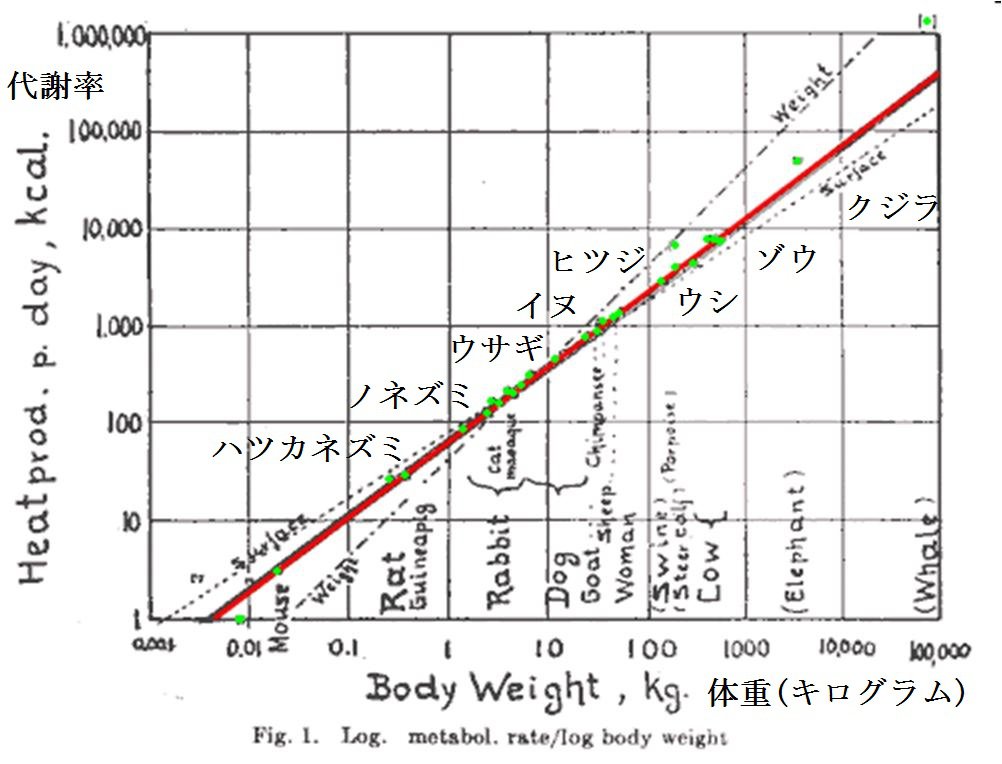
1930年代にカリフォルニア大学デイビス校のマックス・クライバーは、哺乳類の体重と代謝率(たとえばエネルギー消費量)が、ネズミからクジラにいたるまで、
$$ (代謝率) \propto (体重)^{3/4} \ , $$
という関係にあることを発見した。ここで、\(\propto\) というのは、比例しているという記号だ。ネズミの体重はおよそ \(10^{-1}\) キロ、クジラの体重は \(10^5\) キロなので、6桁にわたる関係である。クライバーの法則は、その後80年の間に変温動物にも当てはまることがわかり、さらには、植物や単細胞生物から、ミトコンドリアにいたる27桁の世界に拡張されている。
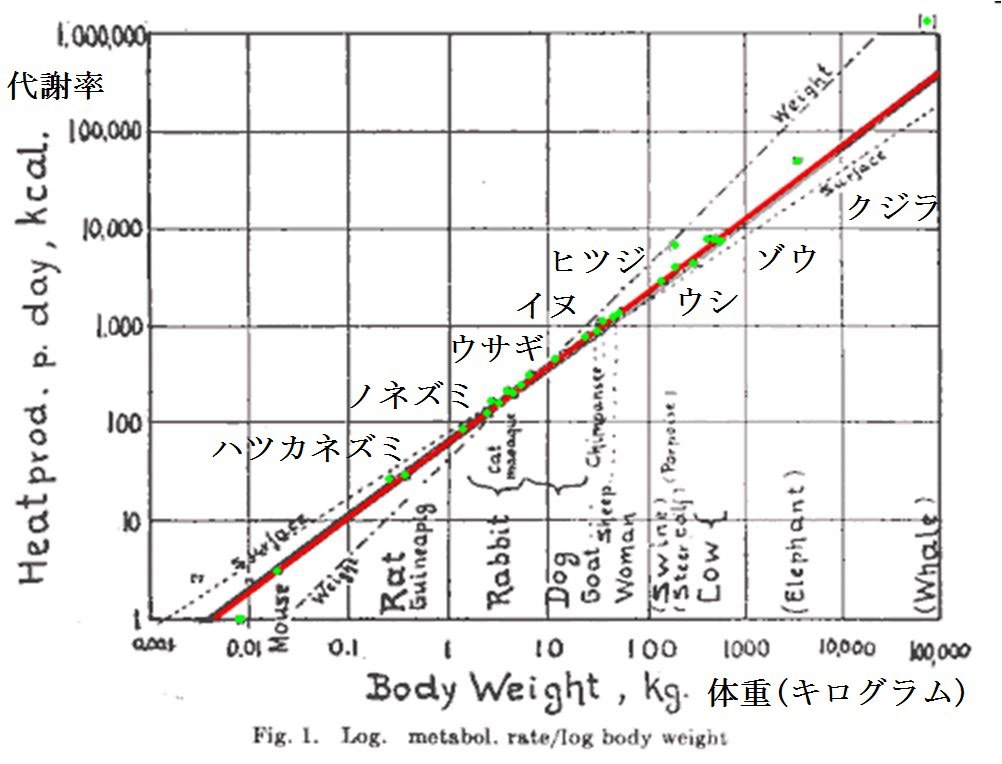
クライバーの法則も対数プロットによって発見された。上の図は、クライバーの1947年の論文の図で、横軸の目盛りは \(\log_{10}(体重)\)、縦軸の目盛りは \(\log_{10}(代謝率)\)。ハツカネズミからクジラにいたるまで、見事に直線に乗っている。対数を使うことで、何桁にもわたるデータから法則を見抜くことができるんだ。
\(\log\)-\(\log\) プロットによって、さまざまなべき乗法則が発見されてきた。たとえば、哺乳類の心拍数はおおむね
$$ (心拍数) \propto (体重)^{-1/4} \ , $$
にしたがっている。体重が大きな動物ほど、心拍数がゆっくりなんだ。また、哺乳類の寿命は、およそ
$$ (寿命) \propto (体重)^{1/4} \ , $$
にしたがっている。そうすると、哺乳類の一生の間の総心拍数、つまり \((心拍数)\times (寿命)\) を考えると、心拍数の \((体重)^{-1/4}\) と寿命の \((体重)^{1/4}\) が相殺するので、どのような種類のものでもほぼ同じ値になる。すべての哺乳類は、一生の間におよそ15億回心拍をすることが知られている。
僕は健康のために、週に3回はジムに行って運動をすることにしているけれど、一生の間の心拍数が決まっているのなら、心拍数を上げるような運動はしない方がよいのだろうか。
べき乗の法則は、人間や動物の社会活動にも見つかっている。ハーバード大学の言語学者ジョージ・ジップは、英語や日本語のような自然言語の文章データで、単語の頻度を調べ、
「ランキングが \(n\) 番目の単語の頻度は、\(n\) に反比例する」
という法則を発見した。たとえば、英語でよく出る単語は、「the」、「of」、 「and」、「to」、…という順番になっているが、ジップの法則によると、「of」の頻度は「the」の1/2、「and」の頻度は1/3、「to」の頻度は1/4となる。都市の人口とその順位、企業の収入とその順位も同じような法則にしたがうそうだ。
このジップの法則と似たものとして、パレートの法則というものもある。イタリアの経済学者ヴィルフレド・パレートが提唱したもので、いろいろなバージョンがあるが、たとえば「売上の8割は、全従業員のうちの2割で生み出している」、「所得税の8割は、課税対象者の2割が担っている」など、ものごとの大部分は、全体を構成するうちの一部の要素が生み出しているという説だ。たとえば、ハタラキアリを観察して、そのなかで最も働き者の2割を選んだエリート集団を作ると、そのなかの8割が怠け者になって、残りの2割だけが働くことになるという。